1. 基础模型架构

首先是一个简单的 linear 专家模型实现：

import torch
import torch.nn as nn
import torch.nn.functional as F

class Linear(nn.Module):
    def __init__(self, in_features, out_features):
        super(Linear, self).__init__()
        self.fc = nn.Linear(in_features, out_features)
    
    def forward(self, x):
        return self.fc(x)
    
class MoELayer(nn.Module):
    def __init__(self, num_experts, in_features, out_features):
        super(MoELayer, self).__init__()
        self.num_experts = num_experts
        self.experts = nn.ModuleList([Linear(in_features, out_features) for _ in range(num_experts)])
        self.gate = nn.Linear(in_features, num_experts)
    
    def forward(self, x):
        gate_score = F.softmax(self.gate(x), dim=-1)
        expert_outputs = torch.stack([expert(x) for expert in self.experts], dim=1)
        output = torch.bmm(gate_score.unsqueeze(1), expert_outputs).squeeze(1)
        return output

实现细节说明

expert_outputs 的张量维度变换

• 各专家模型 expert(x) 输出形状：(batch_size, out_features)
• 使用 torch.stack 沿第 1 维堆叠 num_experts 个专家输出
• 最终得到形状：(batch_size, num_experts, out_features)

torch.bmm 运算过程

• gate_score.unsqueeze(1) 形状：(batch_size, 1, num_experts)
• expert_outputs 形状：(batch_size, num_experts, out_features)
• torch.bmm 要求：输入为 (batch_size, n, m) 和 (batch_size, m, p) 的三维张量
• 输出形状：(batch_size, 1, out_features)
  

2. 相关研究进展

2.1 ViMoE

这篇文章主要探讨了两个核心问题：

1. 专家层数是否越多越好？
   • 答案是否定的
   • 浅层加入专家层效果不理想
   • 深层能较好地处理信息
2. 专家数量是否越多越好？
   • 同样是否定的
   • 作者提出共享专家思路，在保持原有内容的同时引入新特征
     

文章提出了层数与专家数的组合关系：D = (C_N^k)ᴸ

• 组合数量过少会影响模型性能
• 过多则不会带来显著提升

值得进一步探讨的是，目前 top 1 模型损失不连贯，例如在下游任务分割中针对细小边缘区域是否可以吸收其他专家的建议。

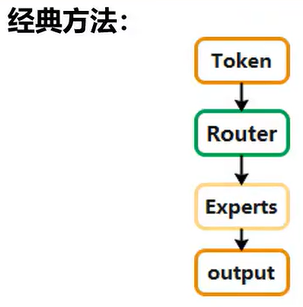
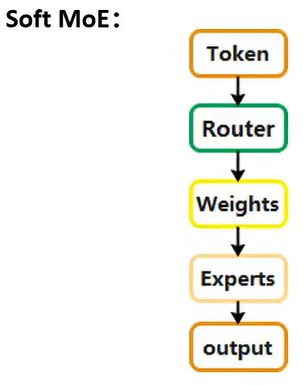
2.2 Soft MoE

主要描述不同特征的加权融合联系。

主要缺点：

• 模型体积较大
• 训练时间仍然较长
  

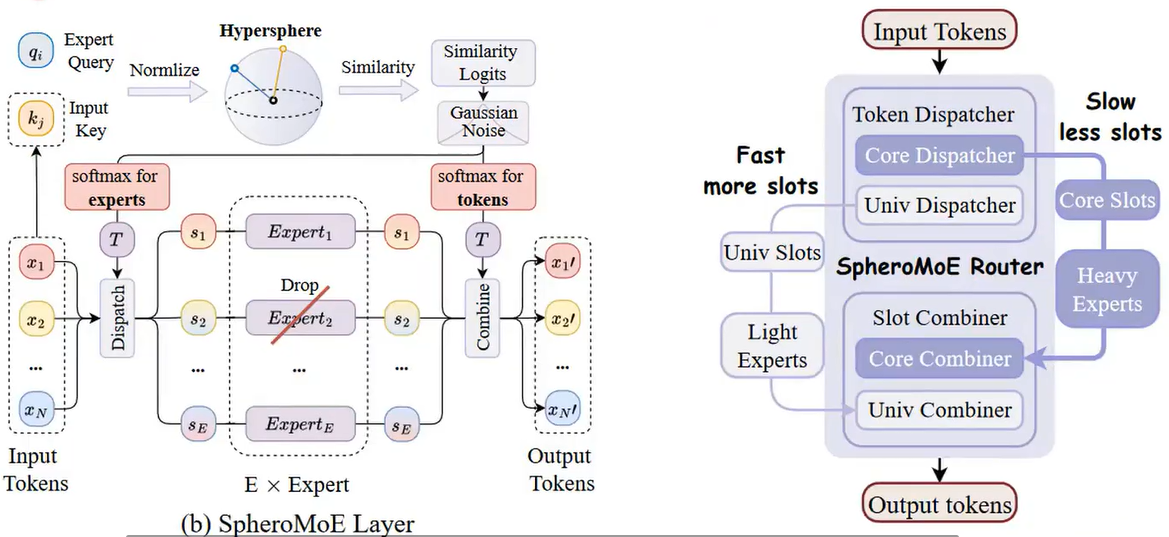
2.3 MoE Jetpack

创新点：

1. 检查点回收机制：通过采样部分权重构建专家，确保专家的多样性

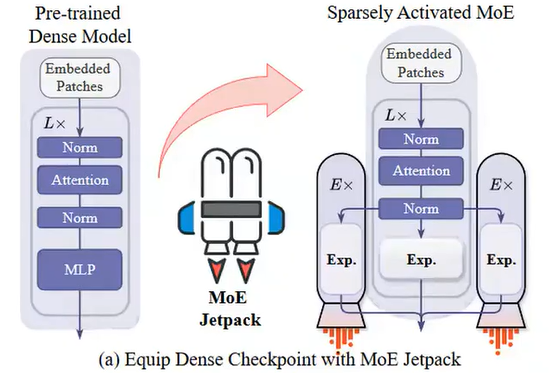
1. 利用交叉注意力机制在各个专家之间分配输入
2. 自适应双路径混合专家：
   • 根据权重大小进行分类
   • 权重大的进入 heavy expert
   • 权重小的进入 light expert

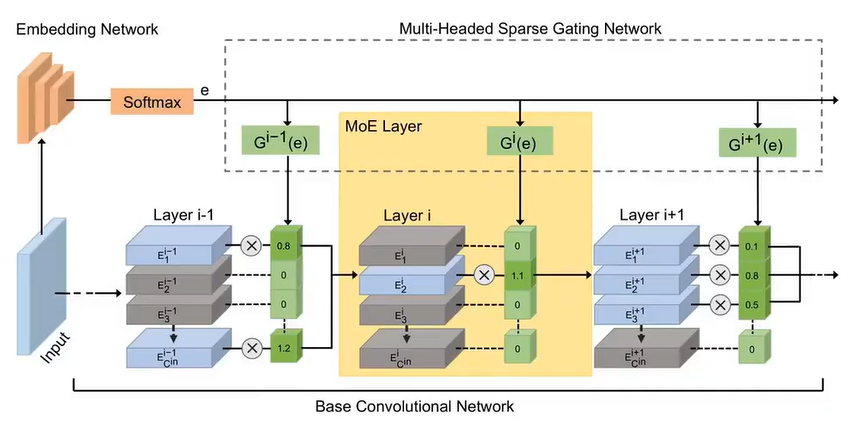
2.4 非 Transformer 结构的 MoE 探索

在 CNN 中将卷积视为 MoE 层：

• 生成权重为 0 的直接丢弃
• 使模型更加轻量化

3. 总结

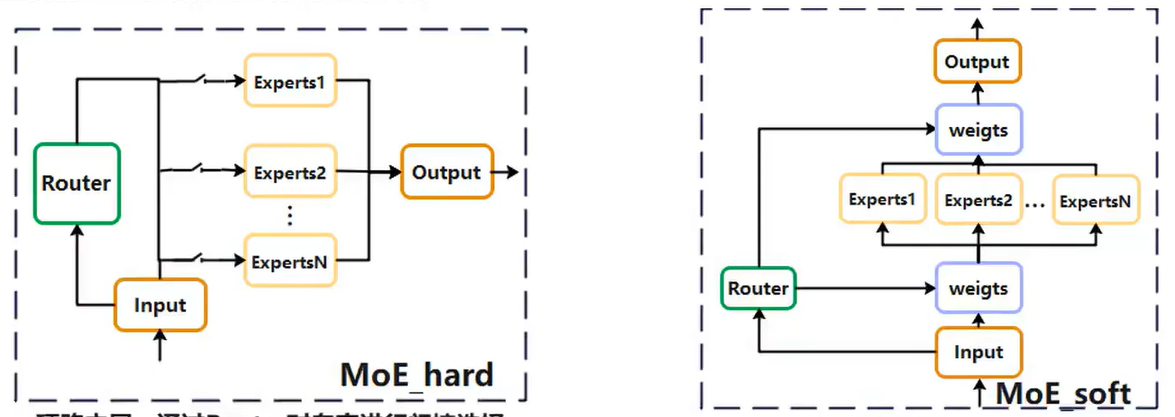
MoE 层结构主要分为两种类型：

1. 通过 router 对专家进行门控选择
2. 通过 router 对专家输入输出进行加权

核心思想始终是”私人订制”。